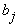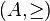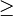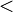Relaciones Reflexivas e
Irreflexivas
Una relación R en un conjunto A
es reflexiva si (a, a) £ R para todas las a £ A, esto es, si a R e
para todas las a e A. Una relación R en un conjunto A es irreflexiva si a R
a para toda a £ A.
Por consiguiente, R es reflexiva si cada elemento a
e A está relacionado consigo mismo y es irreflexiva si ningún elemento está
relacionado consigo mismo.
Ejemplo:
(a) Sea Δ = [(a, a)\ a £ A], de
modo que A es la relación de igualdad en el conjunto A. Entonces A es
reflexiva, ya que (a, a) £ Δ para todas las a e A.
(b) Sea R = {(a, b) e A x A | a + b}, R es la
relación de desigualdad en el conjunto A. Entonces R es irreflexible,
ya que (a, a) £ R para todas las x € A.
(c) Sean A = {1, 2, 3}. y Jí = {(1, 1), (1, 2)}.
Entonces A es reflexiva ya
(2,2) R y (.3,3) € R. Por otra parte, R no es
irreflexiva, ya que (1, l) € R.
(d) Sea A un conjunto no vacio. Sea R
= Ǿ A x A, la relación vacía. Enlaces R no es reflexiva, ya
que (a, a) € R para todas las a € A (el conjunto vacío tiene elementos). Sin
embargo, R es irreflexiva.
Relaciones Simétricas y
Asimétrica
Una relación R en un conjunto A es simétrica si
cuando a R b, entonces b R a. De esto se sigue que R no es simétrica se tiene a
y b € A con a R b, pero b R a. Una relación R en un conjunto A es asimétrica si
cuando a R b, entonces b Ra. De esto se sigue que R no es simétrica si se tiene
a y b e A con ambos a R b y b R a.
Una relación R en un conjunto A es asimétrica si
cuando a R b y b R a, entonces a = b. Otra forma de expresar esta definición es
diciendo que R es anti simétrica si cuando a ≠ b, se tiene a R b o b R a. De
esto se sigue que R no es anti simétrica si se tiene a y b en A. a ≠ b, y ambas
a R b y b R a.
Ejemplo Sea A «= [a, b, c, d, e} y sea R
la relación simétrica dada por
R = {(a, b), (b, a), (a, c), (c, a), (b, c), (c,
b), (b, e), (e, b), (e, a), (a, e), (c,a), (a,c)}
El grafo dirigido de R se muestra en la figura
2(a), mientras que en la figura.
Grafo dirigido de R
Grafo dirigido de R
Aparece el grado de R. Obsérvese
que cada arista no dirigida corresponde a dos pares ordenados en la
relación R.
A una relación simétrica R en un
conjunto A se le llamará conexa si existe una
trayectoria de cualquier elemento de A a cualquier otro elemento
de A. Esto significa sencillamente que el grafo de R está
todo en una pieza. En la figura 3 se muestran los grafos de dos relaciones
simétricas. El grafo de la figura 3(a) está conectado mientras que el de la
figura 3(b) no lo está.
Relaciones Antisimetricas
Una relación binaria 
sobre un conjunto 
es antisimétrica cuando se da que si dos elementos de se relacionan entre sí mediante , entonces estos elementos son iguales.
Es decir,
Para todo a, b de A, si se cumple que a está relacionado con b y b está relacionado con a, entonces a es igual a b.
En tal caso, decimos que cumple con la propiedad de antisimetría.
Representación:
La aplicación de cualquier relación sobre un conjunto , se representa con el par ordenado 
Sea una relación antisimétrica aplicada sobre un conjunto , entonces tiene una representación particular para cada forma de describir una relación binaria.
*Como pares ordenados, 
*Como matriz de adyacencia 
, la matriz 
no tiene ningún 2 salvo, a lo sumo, en la diagonal.
*Como grafo, dos nodos no podrán estar conectados por dos aristas
dirigidas en ambas direcciones. Sin embargo, sí podría tener bucles.
Ejemplo:
Sea un conjunto cualquiera:
*Sea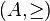 
, 
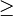("mayor o igual que") es
antisimétrica, al igual que 
("mayor estricto que"), pues
en este último caso, el antecedente de la definición nunca se
cumple.
*Sea 
, 
("menor o igual que") es
antisimétrica, al igual que 
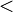("menor estricto que"), pues
en este último caso, el antecedente de la definición nunca se
cumple.
*La relación "ser más alto que" es antisimétrica, pues
el hecho que a sea más alto que b y b sea
al mismo tiempo más alto que a, es imposible.
Antisimetria \neq Simetria:
La antisimetría no es lo opuesto de la simetría.
Existen relaciones que son simétricas y antisimétricas al mismo tiempo
(como la igualdad), otras que no son simétricas ni antisimétricas (como
la divisibilidad para los enteros), otras que son simétricas pero no
antisimétricas (como la relación de congruencia módulo n),
y otras que son antisimétricas pero no simétricas (como la relación "menor
que").
Relaciones Transitivas
Se
dice que una relación R en un conjunto A es transitiva si
cuando a R b y b R e, entonces a R c. Se sigue
que R no es transitiva si y sólo si se puede encontrar
elemento a, b y c en A tal que a R b
y b R c, pero a R c.
Ejemplo: Sea A = Z el conjunto de los enteros y
sea R la relación considerada en el ejemplo 2 Para ver
si R es transitiva, se supone que a R b y b R c. Por
consiguiente, a < b; b < c. Entonces se sigue que a
< c, por lo cual a R c. De aquí que R sea
transitiva.
Una relación R en un conjunto A es transitiva
si y sólo si satisface las siguientes propiedades: Si existe una trayectoria de
longitud mayor que 1 del vértice a al vértice b, hay una
trayectoria de extensión 1 de a a b (esto es, a está
relacionada con b). Establecido algebraicamente, R es transitiva
si y sólo si Rn £ R para todas las n ≥
1.
Es posible caracterizar la relación transitiva por su matriz MR = [mij]
así:
si mij =1 y mjk = 1, entonces mik = 1
Para ver qué significa transitividad en términos del grafo dirigido de
una relación, se traducirá esta definición a términos geométricos.
Si se examinan los vértices particulares a y c, las condiciones a R b y
b R c
ocurrirán
si y sólo si existe una trayectoria de longitud 2 de a a c, esto es, si y sólo
si a R2 c. Es posible replantear la definición de transitividad como sigue: Si
a R2 c, entonces a R c, esto es, R2 £ R (como un subconjunto de A x A).
